[机器学习]04 决策树

决策树是一种分类问题中常用的算法。它是按照一定的顺序选择属性组进行判别，并根据标签值 $y_{i}$ 逐步学习判别规则的一种方法，这种判别规则就是决策树模型。

4.1 基本流程

4.1.1 介绍

策略：分而治之
停止条件：
- 当前结点包含的样本全属于同一类别，无需再分(已经学到某类样本的全部特征了)
- 当前属性集为空，或是所有样本在所有属性上取值相同，无法划分
- 当前结点包含的样本集合为空(是个无用的叶结点)

若停止后，某个叶节点的样本类型还不唯一，则把该叶节点样本中占比最多的类别认为是该节点的类别(判决结果)。

4.1.2 伪代码

决策树伪代码

看这一段很容易懵，别担心，待会看个例题就好了

4.2 划分选择

决策树是一个迭代的、从上往下的“逐渐划分”的过程，决策树越短，迭代次数越少，效率越高。
那么如何让决策过程尽量短呢？从贪心的角度来说，应该优先选择“最能够分开不同类的”特征；从信息论的角度来说，这个应该叫做“信息增益”。

4.2.0 信息熵

信息熵：度量样本集合“纯度”的一种指标(这和中学物理中熵的概念也类似)
假定当前样本集合 $D$ 中第 $k$ 类样本所占的比例为 $p_{k}$ ，则 $D$ 的信息熵定义为：
$E n t (D) = - \sum_{k = 1}^{| γ |} p_{k} \log_{2} p_{k}$
$E n t (D)$ 的值越小，则 $D$ 的纯度越高
可见随着决策树的逐渐划分，信息熵会逐渐降低，直到为0或不可再分

关于该公式的解释：对于一个信息源，它产生的每个事件都有一定的概率和不确定性，我们可以用 $- \log_{2} p (x)$ 来衡量一个事件的不确定性(这个函数和 $p (x)$ 呈反比，概率越低不确定性越高，合理)，然后用所有事件的概率加权平均得到整个信息源的平均不确定性(整体不确定性的期望)，也就是信息熵。

4.2.1 信息增益

基于上一节的信息熵来定义信息增益。本节将展示如何计算信息增益，以及如何选择最优划分属性。

假定属性 $a$ 有 $V$ 个可能的取值 ${a^{1}, a^{2}, \dots, a^{v}}$
那么按照 $a$ 的取值可分出 $V$ 个样本子集(分别记作 $D^{1}, D^{2}, \dots, D^{v}$ ，空集也算)
信息增益实质上就是“按照属性 $a$ 划分后，信息熵的降低量”，但是原本的信息熵 $E n t (D)$ 好算，划分后的 $V$ 个子集的信息熵 $E n t (D^{v})$ 怎么算呢？
- 其实和信息熵的思想类似：计算期望，也就是加权平均。计算每个子集 $D^{i}$ 的信息熵，然后按照每个子集的样本数比例 $\frac{| D^{v} |}{| D |}$ 作为权重计算划分后的平均信息熵。
- 公式表示为：
$G a i n (D, a) = E n t (D) - \sum_{v = 1}^{V} \frac{| D^{v} |}{| D |} E n t (D^{v})$
可见，信息增益越大，说明划分后的平均信息熵越小，这正是我们想要的。因此，我们应该优先选择信息增益最大的属性来划分。
接下来我们看一个信息增益的例题，也就是课本P75～P77的西瓜数据集2.0例题：信息增益例题

4.2.2 增益率

信息增益准则对可取值数目较多的属性有所偏好，为了减少这种偏好可能带来的不利影响，提出了增益率准则。
增益率定义为：
$G a i n_r a t i o (D, a) = \frac{G a i n (D, a)}{IV (a)}$
其中:
$IV (a) = - \sum_{v = 1}^{V} \frac{| D^{v} |}{| D |} \log_{2} \frac{| D^{v} |}{| D |}$
通常随着 $V$ 越大， $IV (a)$ 的值越大，则增益率将响应减小。这个部分可以看作平衡因子，用以平衡信息增益对可取值数目的偏好。(但增益率准则因此对可取数目较少的属性有所偏好....)

4.2.3 基尼系数

基尼系数公式：
$G i n i (D) = \sum^{| γ |} * k = 1 \sum * k^{'} \neq k p_{k} p_{k^{'}} = 1 - \sum_{k = 1}^{| γ |} p_{k}^{2}$
假定数据集 $D$ 中包含 $γ$ 类(西瓜数据集只有2类，好瓜or坏瓜)
- 首先计算各类别的概率 $p_{k}$
- 然后计算各类别两两之间的概率乘积和(不完全握手问题，共有 $γ (γ - 1)$ 个求和项，会同时出现 $p_{i} p_{j}$ 和 $p_{j} p_{i}$ 两项)
直观来说， $G i n i (D)$ 反映了从数据集 $D$ 中随机抽取两个样本，其类别标记不一致的概率。因此， $G i n i (D)$ 越小，则数据集 $D$ 的纯度越高。
与信息熵类似，属性 $a$ 划分后的平均基尼系数为：
$G i n i_i n d e x (D, a) = \sum_{v = 1}^{V} \frac{| D^{v} |}{| D |} G i n i (D^{v})$
所以在使用基尼系数构建决策树时，我们应该优先选择基尼系数降低量最大的属性，也就是平均基尼系数最小的属性：
$a_{*} = \arg min_{a \in A} G i n i_i n d e x (D, a)$

4.3 剪枝处理

鉴于上课时没强调剪枝的事(虽然这个挺重要的其实)，那这里就先不详细讲了，只简单说说大致流程和思想。挖个坑 TODO
上述4.2的选择准则对决策树的尺寸影响较大(模型收敛速度)，但对于泛化性能影响很小(模型的效果)。相比之下，剪枝对泛化性能的影响更大。
剪枝是手动去掉一些分支，用以降低过拟合的风险，提高模型的泛化能力。决策树中的过拟合就是分支过多，误将一些训练集中某些数据的特征当作整个类的整体特征。

剪枝方式：
1. 预剪枝：决策树生成过程中，对每个结点在划分前进行估计，若当前结点的划分不能带来决策树泛化性能提升，则停止划分，将当前结点标记为叶结点。
2. 后剪枝：从训练集生成一棵完整的决策树，然后自底向上地对非叶结点进行考察，若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升，则将该子树替换为叶结点。

4.3.1 预剪枝

基本思想：
- 数据集需要预先划分训练集和测试集，测试集用来计算划分前后的精度。
- 仍然是按照信息增益来选择要划分的属性；但在划分之前，先计算一下当前根结点的测试集精度 $A c c (D)$ ；
- 然后根据该属性划分子结点 ${D_{1}, D_{2}, . . . . D_{γ}}$ ，各个节点使用投票法决定该结点的判断结果。
- 此时可以计算根节点划分后的总精度(根据 $D_{1}, D_{2}, . . . . D_{v}$ 及其判断结果)，如果相较于 $A c c (D)$ 升高了，则该属性划分有效，否则撤销该划分。
- 此时任一叶结点( $D_{i}$ )都可视为一个新的根节点，重复上述过程。

4.3.2 后剪枝

基本思想：
- 同样需要测试集和训练集。后剪枝在构建决策树的过程中不考虑剪枝。
- 等决策树构建完成后，后剪枝逐渐从叶结点向上考查，若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升，则将该子树替换为叶结点。

4.4 连续值和缺失值

4.4.1 连续值处理

例如西瓜数据集中，其实包含了密度和含糖率这两个连续值特征。此时我们的策略是连续值离散化，本节介绍一个最典型的：二分法。

对于某个连续属性 $a$ ，我们首先按照 $a$ 进行排序，然后取连续两个值的中点( $\frac{a_{i} + a_{i + 1}}{2}$ )作为划分点 $t$ ，不大于 $t$ 的算负类 $D_{t}^{-}$ ，大于的算正类 $D_{t}^{+}$
对于 $n$ 个样本，我们就可以得到 $n - 1$ 个候选划分点，这就相当于属性 $a$ 有 $n - 1$ 个离散值，然后再分别按照二分后的信息增益构建决策树。

4.4.2 缺失值处理

对于缺失值，我们要做的主要是：
存在缺失值的情况下如何计算信息增益，以选择构建决策树的属性
结点划分样本时，如果一个样本在这个结点属性上缺失，它该如何划分？
在本节中提出了3个新的变量，并借助这三者解决以上两个问题。

此时每个样本都应当有一个权重 $w_{x}$ (预先给定，如果没给的话默认为 $\frac{1}{n}$ )
原始数据集为 $D$ ，则设 $\tilde{D}$ 为在属性 $a$ 上没有缺失值的样本子集。
然后我们定义以下3个变量：

ρ = \frac{\sum_{x \in \tilde{D}} w_{x}}{\sum_{x \in D} w_{x}}

\tilde{p_{k}} = \frac{\sum_{x \in \tilde{D_{k}}} w_{x}}{\sum_{x \in \tilde{D}} w_{x}}

\tilde{r_{v}} = \frac{\sum_{x \in \tilde{D^{v}}} w_{x}}{\sum_{x \in \tilde{D}} w_{x}}

可以看出，这三者分别是用权重 $w_{x}$ 衡量的无缺样本比例、无缺样本中第 $k$ 类样本比例和无缺样本中第 $v$ 个属性值的样本比例。

(1) 估算信息增益

推广后的信息增益：

G a i n (D, a) = ρ \times G a i n (\tilde{D}, a) = ρ \times (E n t (\tilde{D}) - \sum_{v = 1}^{V} \tilde{r_{v}} E n t (\tilde{D^{v}}))

其中 $E n t (\tilde{D}) = - \sum_{k = 1}^{| γ |} \tilde{p_{k}} \log_{2} \tilde{p_{k}}$

也就是说，先计算无缺信息熵 $E n t (\tilde{D})$ 和各子集信息熵 $E n t (\tilde{D^{v}})$
然后仿照信息增益，计算无缺信息增益 $G a i n (\tilde{D}, a)$ ；在信息增益中的样本量之比 $\frac{| D^{v} |}{| D |}$ 用 $\tilde{r_{v}}$ 代替。
最后无缺信息增益乘以无缺比例 $ρ$ ，估计出原本的信息增益。并根据这个估算的信息增益选择决策树的划分属性。

(2) 缺失样本划分

缺失样本划分的策略是：将缺失样本同时划分到所有子结点，但是权重按照各子结点的样本比例进行分配。
比如样本 $x$ 的属性 $a$ 的值丢失；而属性 $a$ 有 $V$ 个取值，那么样本 $x$ 就会被划分到 $V$ 个子结点中，但各自的权重 $w_{x}$ 分别调整为 $\tilde{r_{1}} w_{x}, \tilde{r_{2}} w_{x}, \dots, \tilde{r_{V}} w_{x}$
- 这能维持样本 $x$ 的 $v$ 个“分身”的权重之和仍然是 $w_{x}$ ，但不太清楚这样做的目的是什么....

Extra04-整理

本章的知识脉络如下

其中，划分选择是本章的大重点，需要会计算信息熵、信息增益、信息增益率、基尼系数，并据此选择构建决策树的划分属性。
连续值和缺失值的处理是小重点，要能够理解二分法和缺失样本划分的策略，公式最好也在理解的基础上记住( 不如说公式能够辅助理解)。
剪枝策略要知道两种策略的思想，可能会出个简答题吧，但实操起来还是比较麻烦的....

Ques04-例题整理

[计算题·使用信息增益划分决策属性]

题目内容

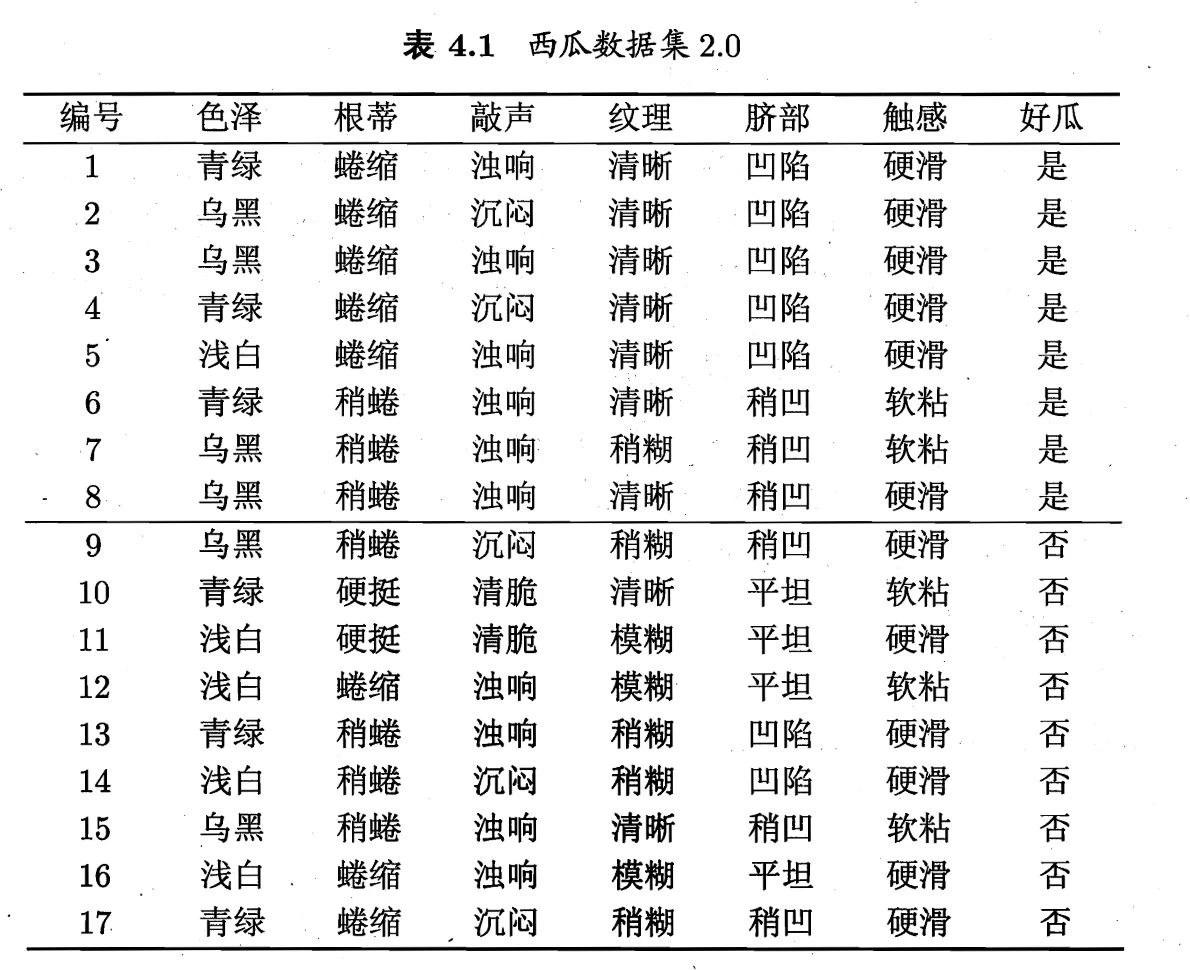
4.2 信息增益例题

假定当前结点的数据如图所示，请计算每个属性的信息增益，然后选择信息增益最大的属性作为划分属性。

分析与解答

只要是涉及了决策树的计算，那运算量通常不会小....
首先明确，西瓜数据集只是个二分类问题，所以只有 $p_{1}$ (正例)和 $p_{2}$ (负例)

(1) 计算 $E n t (D)$

很容易看出正例8个，负例9个，所以 $p_{1} = \frac{8}{17}, p_{2} = \frac{9}{17}$
然后计算初始信息熵：

E n t (D) = - \sum_{k = 1}^{| γ |} p_{k} \log_{2} p_{k} = - \frac{8}{17} \log_{2} \frac{8}{17} - \frac{9}{17} \log_{2} \frac{9}{17} = 0.998

(2) 对6个特征，分别计算划分后的平均信息熵和信息增益

由于对各个特征计算信息增益时被减数( $E n t (D)$ )相同，所以“选择信息增益最大的”等价于“选择划分后平均信息熵最小的”

色泽：青绿={+:3,-:3}=6;乌黑={+:4,-:2}=6;浅白={+:1,-:4}=5
- $E n t (D^{青绿}) = - \frac{3}{6} \log_{2} \frac{3}{6} - \frac{3}{6} \log_{2} \frac{3}{6} = 1$
- $E n t (D^{乌黑}) = - \frac{4}{6} \log_{2} \frac{4}{6} - \frac{2}{6} \log_{2} \frac{2}{6} = 0.918$
- $E n t (D^{浅白}) = - \frac{1}{5} \log_{2} \frac{1}{5} - \frac{4}{5} \log_{2} \frac{4}{5} = 0.722$
- 平均信息熵为： $\sum_{v = 1}^{V} \frac{| D^{v} |}{| D |} E n t (D^{v}) = \frac{6}{17} \times 1 + \frac{6}{17} \times 0.918 + \frac{5}{17} \times 0.722 = 0.889$
- 信息增益为 $G a i n (D, 色泽) = E n t (D) - \sum_{v = 1}^{V} \frac{| D^{v} |}{| D |} E n t (D^{v}) = 0.109$
根蒂
- ......
- 信息增益为 $G a i n (D, 根蒂) = E n t (D) - \sum_{v = 1}^{V} \frac{| D^{v} |}{| D |} E n t (D^{v}) = 0.143$
敲声
- ......
- 信息增益为 $G a i n (D, 敲声) = E n t (D) - \sum_{v = 1}^{V} \frac{| D^{v} |}{| D |} E n t (D^{v}) = 0.141$
纹理：清晰={+:7,-:2}=9;稍糊={+:1,-:4}=5;模糊={+:0,-:3}=3
- $E n t (D^{清晰}) = - \frac{7}{9} \log_{2} \frac{7}{9} - \frac{2}{9} \log_{2} \frac{2}{9} = 0.764$
- $E n t (D^{稍糊}) = - \frac{1}{5} \log_{2} \frac{1}{5} - \frac{4}{5} \log_{2} \frac{4}{5} = 0.722$
- $E n t (D^{模糊}) = 0$
- 平均信息熵为： $\sum_{v = 1}^{V} \frac{| D^{v} |}{| D |} E n t (D^{v}) = \frac{9}{17} \times 0.764 + \frac{5}{17} \times 0.722 + \frac{3}{17} \times 0 = 0.617$
- 信息增益为 $G a i n (D, 纹理) = E n t (D) - \sum_{v = 1}^{V} \frac{| D^{v} |}{| D |} E n t (D^{v}) = 0.381$
脐部
- ......
- 信息增益为 $G a i n (D, 脐部) = E n t (D) - \sum_{v = 1}^{V} \frac{| D^{v} |}{| D |} E n t (D^{v}) = 0.289$
触感
- ......
- 信息增益为 $G a i n (D, 触感) = E n t (D) - \sum_{v = 1}^{V} \frac{| D^{v} |}{| D |} E n t (D^{v}) = 0.006$
因为纹理的信息增益最大，所以选择纹理作为划分属性

至此完成了一次迭代，然后分别对上图所示的3个结点重复上述操作。注意此时根节点是上述你选择叶结点；也就是说如果从上述“清晰”结点开始， $D = {1, 2, 3, 4, 5, 6, 8, 10, 15}$ ，而非先前的17个

Reference

决策树：什么是基尼系数（“杂质增益指数系数”辨析）_决策树基尼系数_loopy_的博客-CSDN博客

[机器学习]04 决策树 ​

4.1 基本流程 ​

4.1.1 介绍 ​

4.1.2 伪代码 ​

4.2 划分选择 ​

4.2.0 信息熵 ​

4.2.1 信息增益 ​

4.2.2 增益率 ​

4.2.3 基尼系数 ​

4.3 剪枝处理 ​

4.3.1 预剪枝 ​

4.3.2 后剪枝 ​

4.4 连续值和缺失值 ​

4.4.1 连续值处理 ​

4.4.2 缺失值处理 ​

(1) 估算信息增益 ​

(2) 缺失样本划分 ​

Extra04-整理 ​

Ques04-例题整理 ​

[计算题·使用信息增益划分决策属性] ​

(1) 计算Ent(D) ​

(2) 对6个特征，分别计算划分后的平均信息熵和信息增益 ​

Reference ​

[机器学习]04 决策树

4.1 基本流程

4.1.1 介绍

4.1.2 伪代码

4.2 划分选择

4.2.0 信息熵

4.2.1 信息增益

4.2.2 增益率

4.2.3 基尼系数

4.3 剪枝处理

4.3.1 预剪枝

4.3.2 后剪枝

4.4 连续值和缺失值

4.4.1 连续值处理

4.4.2 缺失值处理

(1) 估算信息增益

(2) 缺失样本划分

Extra04-整理

Ques04-例题整理

[计算题·使用信息增益划分决策属性]

(1) 计算 $E n t (D)$

(2) 对6个特征，分别计算划分后的平均信息熵和信息增益

Reference