[机器学习]03 线性模型

本章介绍最简单、最入门的模型——线性模型

3.1 基本形式

• 线性模型的基本形式为：$f(x)={\omega }_1{x}_1+{\omega }_2{x}_2+...+{\omega }_d{x}_d+b$
• 用向量表示为：$f(x)={\omega }^{T}x+b$，其中$\omega =({\omega }_1,{\omega }_2,...,{\omega }_d{)}^T$

可以看出，当$\omega$和$b$确定后，线性模型就确定了，所以本章接下来的任务就是花式确定$\omega$和$b$。

3.2 线性回归

均方误差：戳这里回顾一下

• 在做线性回归之前，我们要先确定一点：什么样的线性函数是好的？
  • 根据我们朴素的想法：如果这条函数直线经过所有点，那它就是好的。确实，但前提是这得是有可能的。
  • 如果不存在经过所有点的直线，那这条直线至少能够尽量接近所有点，即要求“偏差最小”(这个表述有些不严谨)。
  • 如何去衡量这个偏差呢？首先想到的应该是点到直线的欧氏距离。广义最小二乘法(GLS)就是以欧氏距离为偏差，最小化偏差的平方和(即均方误差)。不过由于点到直线的距离计算起来比较麻烦，大多数时候我们仅使用输出值$y$这个维度的距离($f(x_i)-y_i$)作为偏差，这就是普通最小二乘法(OLS)。
  • 事实上我们本章只需要知道OLS即可，因为平时也只使用OLS，平时说“最小二乘法”也是指的普通最小二乘法。

3.2.1 最小二乘的参数估计

这其实就是个优化问题，不过存在闭式解，这里介绍闭式解的推导过程。

闭式解：通过数学推导，得出的解析解，它可以保证计算结果就是最优解(而梯度下降等方式求出的只是逼近最优解的可行解)。

(1) 问题分析

• 对于线性回归函数$f(x_i)=\omega x_i+b$，我们的目标是求出最优的$\omega$和$b$(记作${\omega }^{\ast }$和$b^{\ast }$)，使得$E_{(\omega ,b)}=\sum _{i=1}^m(f(x_i)-y_i{)}^2$最小。这个过程可以视为对于一个函数$E(\omega ,b)$求极值的问题，表示为$({\omega }^{\ast },b^{\ast })=ar{g}_{(\omega ,b)}min\sum _{i=1}^m(y_i-\omega x_i-b{)}^2$

根据高数的老套路，对变量分别求偏导，偏导均为0时，即为极值点。

• 求偏导：
  • $\frac{\partial E_{(\omega ,b)}}{\partial \omega }=2(\omega \sum _{i=1}^m{x}_i^2-\sum _{i=1}^m(y_i-b)x_i)$
  • $\frac{\partial E_{(\omega ,b)}}{\partial b}=2(mb-\sum _{i=1}^m(y_i-\omega x_i))$
• 令上式=0，解方程得：
  • ${\omega }^{\ast }=\frac{\sum _{i=1}^m{y}_i(x_i-\overline{x})}{\sum _{i=1}^m{x}_i^2-\frac{1}{m}(\sum _{i=1}^m{x}_i{)}^2}$
  • $b^{\ast }=\frac{1}{m}\sum _{i=1}^m(y_i-\omega x_i)=\overline{y}-\omega \overline{x}$
• 上述结果就是闭式解，这是能正向直接算出来的，而不需要迭代。

(2) 解法优化

其实就是矩阵化，矩阵化之后不仅更美观，而且可以解决多元线性回归

• 上述的解法已经能够解决问题了，$x_i$不仅可以是标量，也可以是向量——理论上这就能解决任何线性回归问题了。

• 但仔细想想，上述解法还不够优雅。既然$x_i$都是向量了，为什么还要将$\omega ,b$表示为向量+标量的形式呢？对的，解法优化就是将上述运算矩阵化。

  设有$m$组样本$x_i$，每个样本$x_i$都是$d$维。好，接下来推导过程中注意设的新变量。

  • 令$\hat{\omega }=(\omega ;b)$，拼成列向量，此时$\hat{\omega }$有$(d+1)$维，$\hat{\omega }=[{\omega }_1,{\omega }_2,...{\omega }_d,n{]}^T$
  • 令$X$为一个$m\times (d+1)$的矩阵，它是由$x_i$最后增添一个1，然后转置后拼成的。
  $$X=\left[\begin{array}{ccccc}{x}_{11}& x_{12}& \dots & x_{1d}& 1\\ x_{21}& x_{22}& \dots & x_{2d}& 1\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ x_{m1}& x_{m2}& \dots & x_{md}& 1\end{array}\right]=\left[\begin{array}{cc}{x}_1^T& 1\\ x_2^T& 1\\ ⋮& ⋮\\ x_m^T& 1\end{array}\right]$$
  • 此时$Y$为一个列向量，维度为$m$。
  • 此时该问题表示为${\hat{\omega }}^{\ast }=ar{g}_{\hat{\omega }}min\sum _{i=1}^m(Y-X\hat{\omega }{)}^T(Y-X\hat{\omega })$

• 对$\hat{\omega }$求导，得：$\frac{\partial E_{(\hat{\omega })}}{\partial \hat{\omega }}=2X^T(X\hat{\omega }-y)$

• 令上式=0，解方程得：${\hat{\omega }}^{\ast }=(X^{T}X{)}^{-1}{X}^{T}y$

• 这就是最小二乘法的矩阵解法，它仍然是闭式解，理论上能计算出最优解。

• 但很明显，它足够优雅，但不够好用。一方面因为$(X^{T}X{)}^{-1}$的计算难度挺大，另一方面它要求$X^{T}X$满秩，不然有可能解出多个${\hat{\omega }}^{\ast }$。

• 从实用的角度出发，我们需要一个通用、简单的解法，而不一定非得理论上完美，那么这种解法就是迭代类方法，它被广泛用在对数线性回归、逻辑回归等问题中。

3.2.2 对数线性回归

其实就是$y$与$x$不为线性关系，而是指数关系。

这一小节就是为下面的“对数几率回归”做铺垫的

• 若$y\propto e^{{\omega }^{T}x+b}$，则可以等价写成$\ln y={\omega }^{T}x+b$，这样一个函数就是对数线性回归函数。
• 推广来讲，凡是满足$y=g^{-1}({\omega }^{T}x+b)$的函数，都可称之为“广义线性函数”，其中函数$g(·)$称为联系函数”。
• 这时候又想起模式识别老师常说的一句话：“广义线性函数是线性函数吗？”答案是否定的；这里也是，对数线性回顾属于广义线性回归，但它不是线性的。

3.3 对数几率回归

本节我们讨论线性模型如何解决分类问题

虽然它叫“对数几率回归”，但实际上它是一个分类问题，而非回归问题。从名字上也能见端倪：“几率”嘛，一般是预测类别(分类)时才有的概念，回归问题一般是预测个数值，哪有什么“几率”。

• 对于二分类问题，线性模型只需要回答“是”或“否”的问题，因此我们需要将线性模型的输出值转换为“是”或“否”的布尔值。
  • 由于多分类问题都可以视为二分类问题的组合，因此我们只讨论二分类问题，后面会看到如何组合的。

3.3.1 单位阶跃函数

这个函数不重要，只是为了引出$Logistic$函数

• 关于如何让线性回归模型$z={\omega }^{T}x+b$输出分类结果，可能最先想到的解决办法是单位阶跃函数：

$$y=\{\begin{array}{cc}1& z>0;\\ 0.5& z=0;\\ 0& z<0;\end{array}$$

• 当$z>0$时判断为正例，$z<0$时判断为负例，$z=0$时可任意判别。
• 但是单位阶跃函数不连续，数学性质不够优秀(比如不可导)，因此不适合用于机器学习。我们期望能找到一个连续可导函数，能将$(-\mathrm{\infty },+\mathrm{\infty })$映射到$(0,1)$，$Logistic$函数就是这样一个函数。

3.3.2 Logistic函数

也叫“逻辑函数”

• Logistic函数是一个S型函数，它的数学表达式为：

$$\sigma (z)=y=\frac{1}{1+e^{-z}}$$

• 它的图像如下：

  • 
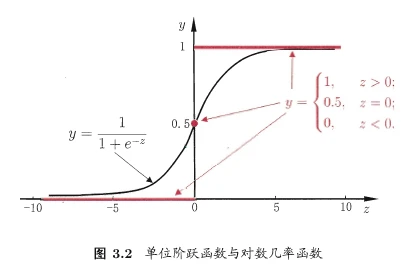
  • 它的优势十分明显：
    • 判别规则十分简单
    • 输出了这一判别的概率
    • 连续可导

• 我们将线性回归函数代入可得$y=\frac{1}{1+e^{-({\omega }^{T}x+b)}}$，这就是$Logistic$回归模型，同样可见，它也是个对数线性模型。

  • 进行同样的取$\ln$操作，并整理，得到$\ln \frac{y}{1-y}={\omega }^{T}x+b$。

• 此外，Logistic还有个特殊性质：它的导数可以用它自己表示：$\frac{\partial \sigma (z)}{\partial z}=\sigma (z)\cdot (1-\sigma (z))$，不信可以自己代入算一下。这个性质也是手算Logistic回归的重要工具。

• 题外话：Sigmoid函数是一类函数，即形似S的函数。Logistic函数就是Sigmoid函数的代表。往后如果不说的话，二者都认为是这个表达式。

3.3.3 解法demo

然后从考试的角度来说，由于公式比较复杂，且十分难算，所以应该不会考这里

仍然是以0-1二分类问题为例。这里用到了极大似然法，后面会讲到。

• 令$\beta =(\omega ;b),\hat{x}=(x;1)$，则${\omega }^{T}x+b$可简写为${\beta }^T\hat{x}$。(这一步的目的是简化表示形式)
• 再令：

$$p_1(\widehat{x_i};\beta )=p(y=1|\hat{x};\beta )=\frac{e^{{\omega }^{T}x+b}}{1+e^{{\omega }^{T}x+b}}$$$$p_0(\widehat{x_i};\beta )=p(y=0|\hat{x};\beta )=\frac{1}{1+e^{{\omega }^{T}x+b}};(\text{其实也就是}1-p_1(\widehat{x_i};\beta ))$$

其实就是把${\beta }^T\hat{x}$代入了$Logistic$函数中，注意到此时表达式形式为条件概率，即在当前$\hat{x},\beta$的条件下，判定$y=1\text{或}y=0$的概率，这正是我们所需的。

• 则似然项可重写为$p(y_i|x_i;{\omega }_i,b)=y_i{p}_1(\widehat{x_i};\beta )+(1-y_i)p_0(\hat{x};\beta )$

  • 多观察一下就能发现，此式形式上就是计算期望。因为$y_i$只能取0或1，所以当$y_i=0$时，概率之前取$1-y_i$作为系数。

• 对于上述似然项(期望)，当然是越大说明模型效果越好，所以该问题转化为一个优化问题：$max\ell (\omega ,b)=\sum _{i=1}^m\ln p(y_i|x_i;\omega ,b)$
• 等价于最小化$\ell (\beta )=\sum _{i=1}^m(-y_i{\beta }^T\widehat{x_i}+\ln (1+e^{{\beta }^T\widehat{x_i}}))$，而对于该式，可使用梯度下降法、牛顿法等方法求解最优解。

3.4 线性判别分析

线性判别分析从功能上可以视作一种降维，其思想和实质都和PCA有些类似。但LDA和PCA的最主要的区别在于：PCA是无监督学习，它要求数据点整体尽可能分开，也就是最大化投影方差；而LDA是有监督学习，它要求投影后类间方差最大，类内方差最小。

对于本节，考试不要求运算，但是要求理解思想。

• LDA的思想非常朴素：给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离。

• 给定数据集:$D=\{(x_i,y_i){\}}_{i=1}^m$

  • 第$i$类示例的集合$X_i$
  • 第$i$类示例的均值向量${\mu }_i$
  • 第$i$类示例的协方差矩阵${\mathrm{\Sigma }}_i$
  • 两类样本的中心在直线上的投影:${\omega }^T{\mu }_0$和${\omega }^T{\mu }_1$

• 则LDA的目标为：使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离,公式可表示为

$$min{\omega }^T{\mathrm{\Sigma }}_0\omega +{\omega }^T{\mathrm{\Sigma }}_1\omega$$$$max||{\omega }^T{\mu }_0-{\omega }^T{\mu }_1|{|}_2^2$$

• 把这两个结合起来可以得到优化的总目标:

$$maxJ=\frac{||{\omega }^T{\mu }_0-{\omega }^T{\mu }_1|{|}_2^2}{{\omega }^T{\mathrm{\Sigma }}_0\omega +{\omega }^T{\mathrm{\Sigma }}_1\omega }=\frac{{\omega }^T({\mu }_0-{\mu }_1)({\mu }_0-{\mu }_1{)}^T\omega }{{\omega }^T({\mathrm{\Sigma }}_0+{\mathrm{\Sigma }}_1)\omega }$$

• 然后咱们首先引入两个矩阵:
  • 类内散度矩阵:$S_{\omega }={\mathrm{\Sigma }}_0+{\mathrm{\Sigma }}_1$
  • 类间散度矩阵:$S_b=({\mu }_0-{\mu }_1)({\mu }_0-{\mu }_1{)}^T$
• 优化目标可化为:$J=\frac{{\omega }^T{S}_b\omega }{{\omega }^T{S}_{\omega }\omega }$,这个又叫做广义瑞利商

3.4.1 总结

• OK我们总结一下:
  • LDA的核心思想是:将样例投影到一条直线上，使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离。
  • 优化目标是最大化广义瑞利商,通常优化方法为拉格朗日乘子法

3.5 多分类问题

前面说过，多分类问题都可以视为二分类问题的组合(或者说多分类问题可以拆解为若干个二分类问题)，这节就正是做这个事的。

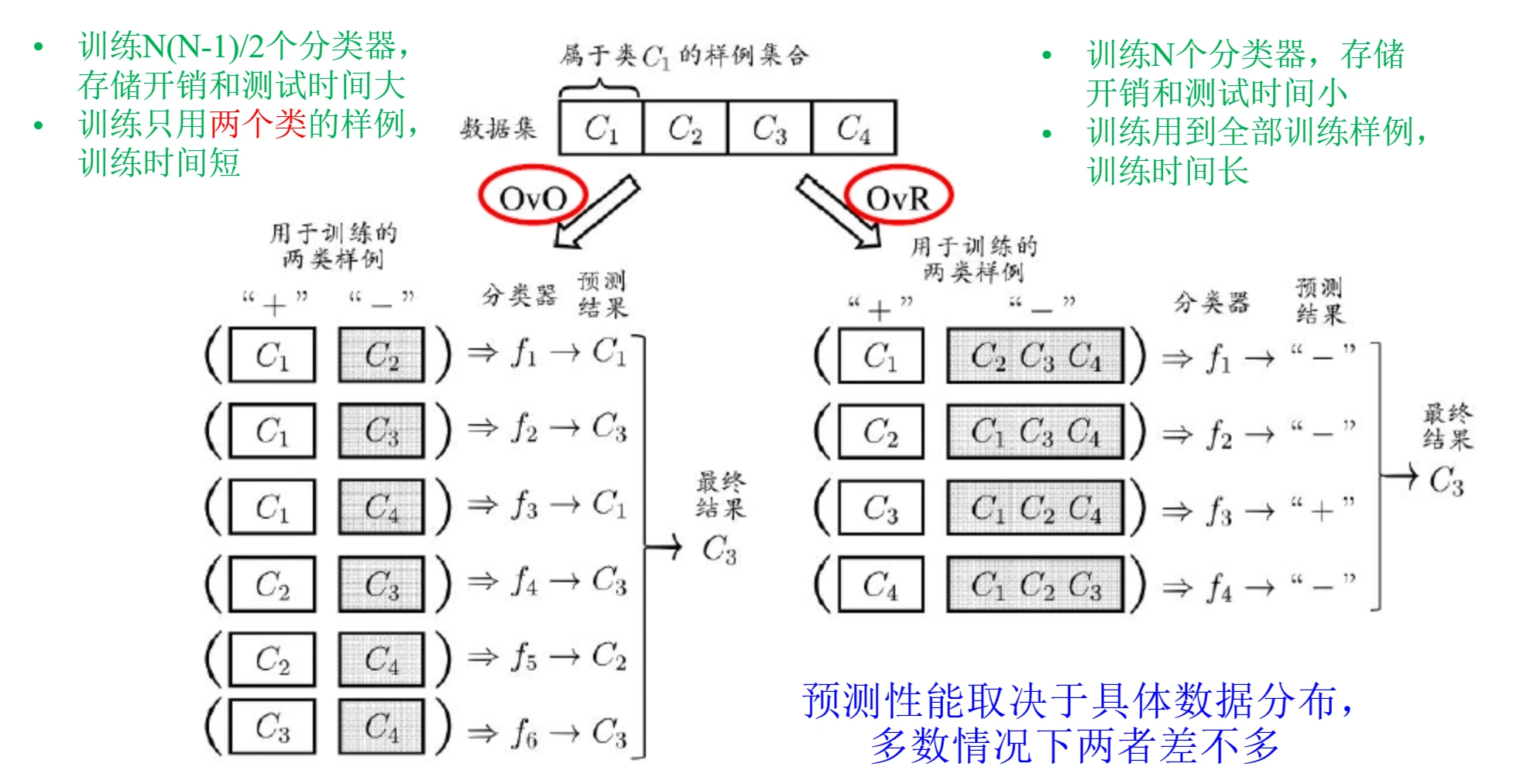
本节的3种拆分策略：“一对一”(One vs. One, OvO)、“一对其余”(One vs. Rest, OvR)、“多对多”(Many vs. Many, MvM)。

• 本节假定：数据集$D=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_m,y_m)\},y_i\in \{C_1,C_2,\cdots ,C_N\}$，即数据集包括了$m$组数据，共有$N$个类别。

3.5.1 OvO

(1) OvO的思想

• 将$N$个类别两两组合(握手问题)，组合出共$\frac{N(N-1)}{2}$个二分类器$f_k$。
• 训练时将$C_i$和$C_j$类数据用以训练分类这两类的分类器。
• 测试时将某样本同时提交给所有分类器，最后根据这$\frac{N(N-1)}{2}$个结果，按照投票数最多的类别作为最终判别结果。

(2) OvO的优缺点

• 优点：训练时间短(每个分类器都是二分类问题，并且只需要和该分类器相关的数据即可)
• 缺点：存储开销和测试时间大($\frac{N(N-1)}{2}$个分类器，且每次测试都要执行这么多次分类)

3.5.2 OvR

(1) OvR的思想

• 设计$N$个分类器，每个分类器$f_i$都只做一个问题：当前样本$x_j$是属于$C_i$类还是其他类。
• 测试时将样本提交给每个分类器。
  • 若只有一个分类器预测为正例，则该样本属于该分类器对应的类别。
  • 若有多个分类器预测为正例，则通常考虑各分类器的预测置信度，选择置信度最高的类别作为最终判别结果。

(2) OvR的优缺点

• 优点：相较于OvO，只训练N个分类器，存储和测试开销小。
• 缺点：训练时间长(训练时要用到全部训练数据)

3.5.3 MvM

• 那么很明显了，MvM就是每个分类器将判断若干个类作为正类，其余作为负类，但是它的正反类必须有特殊的设计，不能随意选取。这里介绍一下最常用的MvM技术：输出纠错码(Error Correcting Output Codes, ECOC)。

3.5.4 ECOC

ECOC的主要步骤为编码和解码。其过程需要结合MvM的具体过程解释。

• 编码：$M$个分类器，每个分类器都将若干个类作为正类，其余作为负类，这$M$个分类器的判定结果组合起来就是该样本的ECOC码。
• 解码：$M$个分类器分别对测试样本进行预测，每个分类器都会返回一个预测标记，共返回$M$个标记，这$M$个标记就是该样本的ECOC码，通常将其中距离最小的类别作为最终判别结果。
  • 二元ECOC码:预测标记是+1或-1;
  • 三元ECOC码:预测标记为+1、-1、0;
  • 此外距离也可以用欧氏距离或海明距离等来衡量。
• 我知道这么说有点懵,那么看看下面的例子：
  • 
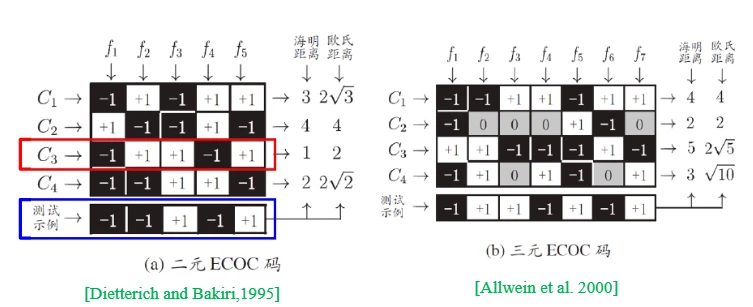
  • 以图(a)为例，有5个分类器，前4行表示这5个分类器$f_i$分别对4个类$C_j$的预测标记.我们能看出,每个分类器$f_i$对不同的类$C_1-C_4$只能返回2种判断结果,即正例or负例.
  • 第5行，对于一个测试用例，这些分类器分别返回相应的预测标记,构成测试用例的ECOC码。然后拿这个码与前面各类的码进行比较，距离最近的类就是最终判别结果。
  • 图(a)中直接给出了测试示例与各类的距离。按照海明距离和欧氏距离，最近的都是$C_3$，所以最终判别结果为$C_3$。而对于(b)来说，海明距离和欧氏距离最近的都是$C_2$，所以最终判别结果为$C_2$。
• ECOC编码的好处在于它对于单个分类器的错误有一定的容忍能力，它的思想有些类似于Boosting,也是训练若干个弱分类器,然后用类似投票的方式实现判决。

3.6 类别不平衡问题

咕咕咕

Extra03-总结

• 本章的知识脉络如下

Ques03-例题整理

[公式推导·利用逻辑回归求导性质]

题目内容

• 对于逻辑回归模型:

$$h_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}x}}$$

• 其损失函数为:

$$J(\theta )=-\frac{1}{m}\sum _{i=1}^m[y^{(i)}\log (h_{\theta }(x^{(i)}))+(1-y^{(i)})\log (1-h_{\theta }(x^{(i)}))]$$

• 其中$m$为样本总数，$y_i$表示第$i$个样本的标签，$x_i$表示第$i$个样本的特征向量，$\theta$为模型参数，$\theta$与$x_i$均为$k$维向量。对于损失函数梯度，我们有

$$\mathrm{\nabla }J(\theta )=\left[\begin{array}{c}\frac{\partial J(\theta )}{\partial {\theta }_1}\\ \frac{\partial J(\theta )}{\partial {\theta }_2}\\ ⋮\\ \frac{\partial J(\theta )}{\partial {\theta }_k}\end{array}\right]$$

• 请计算$\frac{\partial J(\theta )}{\partial {\theta }_j}$并给出详细推导过程。

分析与解答

• 这一题要使用Logistic函数的求导性质.

(1) Logistic函数的导数性质

• 设中间变量$z={\theta }^{T}x$,则

  $$h_{\theta }(x)=\frac{1}{1+e^{-z}}$$$$\frac{\partial h_{\theta }(x)}{\partial z}=\frac{\partial }{\partial z}\left[\frac{1}{1+e^{-z}}\right]=\frac{e^{-z}}{(1+e^{-z}{)}^2}=\frac{1}{1+e^{-z}}\cdot \frac{e^{-z}}{1+e^{-z}}=h_{\theta }\left(x\right)(1-h_{\theta }\left(x\right))$$

这个式子稍后会用.

• 然后我们按照$\frac{\partial J(\theta )}{\partial {\theta }_j}=\frac{\partial J(\theta )}{\partial z}\cdot \frac{\partial z}{\partial {\theta }_j}$的两部分来计算
• $\frac{\partial z}{\partial {\theta }_j}$好算,因为$z={\theta }^{T}x$,所以$\frac{\partial z}{\partial {\theta }_j}=x_j$

(2) 计算$\frac{\partial J(\theta )}{\partial z}$

$$\frac{\partial J\left(\theta \right)}{\partial z}=\frac{\partial }{\partial z}[-\frac{1}{m}\sum _{i=1}^m[y^{\left(i\right)}log\left(h_{\theta }\left(x^{\left(i\right)}\right)\right)+(1-y^{\left(i\right)})log(1-h_{\theta }\left(x^{\left(i\right)}\right))]]$$$$=-\frac{1}{m}\sum _{i=1}^m[y^{\left(i\right)}\frac{1}{h_{\theta }\left(x^{\left(i\right)}\right)}\frac{\partial h_{\theta }\left(x^{\left(i\right)}\right)}{\partial z}-(1-y^{\left(i\right)})\frac{1}{1-h_{\theta }\left(x\left(i\right)\right)}\frac{\partial h_{\theta }\left(x^{\left(i\right)}\right)}{\partial z}]$$

将$\sigma$和常数项提出来,然后内部计算了一个$\log$求导.以$\frac{\partial \log (h_{\theta }(x^{(i)}))}{\partial z}$为例,这个式子可以写成$\frac{\partial \log (h_{\theta }(x^{(i)}))}{\partial h_{\theta }(x^{(i)})}\cdot \frac{\partial h_{\theta }(x^{(i)})}{\partial z}$,前者即为$\frac{1}{h_{\theta }(x^{(i)})}$($y=log(x)$求导嘛)

$$=-\frac{1}{m}\sum _{i=1}^m[y^{\left(i\right)}(1-h_{\theta }\left(x^{\left(i\right)}\right))-(1-y^{\left(i\right)})h_{\theta }\left(x^{\left(i\right)}\right)]$$

这一步就是将Logistic函数的导数性质代入了,不多赘述

$$=\frac{1}{m}\sum _{i=1}^m(h_{\theta }\left(x^{\left(i\right)}\right)-y^{\left(i\right)})$$

简单合并同类项

(3) 计算$\frac{\partial J(\theta )}{\partial {\theta }_j}$

$$\frac{\partial J\left(\theta \right)}{\partial {\theta }_j}=\frac{\partial J\left(\theta \right)}{\partial z}\frac{\partial z}{\partial {\theta }_j}=\left[\frac{1}{m}\sum _{i=1}^m(h_{\theta }\left(x^{\left(i\right)}\right)-y^{\left(i\right)})\right]x_j=\frac{1}{m}\sum _{i=1}^m(h_{\theta }\left(x^{\left(i\right)}\right)-y^{\left(i\right)})x_j^{\left(i\right)}$$

不过说真的.如果真的考场上推个这玩意,那我觉得有点太爆炸了;考场上顶多现场推个Logistic函数求导的性质.

[公式理解·线性模型公式理解]

题目内容

• 对于线性回归模型$f\left(x\right)=w^{T}x+b$，试解析在什么情况下可以消去线性回归的偏置项$b$

分析与解答

• 根据最小二乘法可知，$w={\left(X^{T}X\right)}^{-1}{X}^{T}y$，$b=y-w^{T}X$，当$\overline{X}=0$时，$b=\overline{y}$。此时对于所有样本，设$y^{\prime (i)}=y^{(i)}-b=y^{(i)}-\overline{y}$作为新的目标值，则此时回归模型函数可用$g\left(x\right)=w^{T}x$代替$f\left(x\right)=w^{T}x+b$，消去偏置项$b$以简化运算。