Steven's Blog

[数据结构]06 树和二叉树

面试做算法题时才头疼起来....热热也许还能吃

2023-10-19 14:00 Steven-Zhl

作为有较高难度且使用相对广泛的一种数据结构，树结构一直是备受算法题青睐的数据结构之一。这一篇是一个简单的树结构的笔记。

不过本篇相对于常规的课本内容，会将更多注意力放在代码实现上。我会用尽可能多的编程语言实现，请期待吧。

这是一个典型的树结构

1. 基本概念

符号约定：

• $n$：结点数
• $n_i$：度为$i$的结点数，$n_0$即为叶子结点个数

1.1 树相关的定义

• 在任意一棵非空树中：
  • 有且仅有一个特定的称为根（Root）的结点；
  • 当$n>1$时，任意一个结点及其子结点又构成一棵树(可见树其实是一个递归定义)；
• 结点：树的基本组成单位，包含数据元素及若干指向其子树的分支；
• 结点的度：结点拥有的子树的个数；(注意，与图不同，树的度仅考虑子树，而不考虑父结点)
• 终端结点/叶子结点：度为0的结点；
• 非终端结点/分支结点：度不为0的结点；
• 子结点/父结点：这是一对相对的概念，结点$root$的子结点是$root$的子树的根结点，$root$是任一子结点的父结点；
• 兄弟结点：具有相同父结点的结点互为兄弟结点；
• 祖先/子孙：这也是一对相对的概念，只要结点$root$层数比结点$node$小，且存在直连二者的路径，那么$root$就是$node$的祖先，$node$是$root$的子孙；
• 层次：根结点的层数为1，其余结点的层数等于其父结点的层数加1；
• 深度：最大层次
• 森林：若干个不重叠的树的集合

例题：例题1

1.2 二叉树

二叉树可以说是在树类数据结构中最常用、最常考的类型

• 二叉树：每个结点至多有两颗子树，且子树区分左右

1.2.1 二叉树的性质

• 二叉树第$i$层最多有$2^{i-1}$个结点($i \geq 1$)
• 深度为$k$的二叉树最多有$2^k-1$个结点($k \geq 1$)

  考虑最多情况：1,2,4,8….等比数列求和而已，套公式得出的就是这个。

• 对任意一棵二叉树$T$，若其叶结点数为$n_0$，度为2的结点数为$n_2$，则$n_0=n_2+1$；

  证明：

  • 设$n_1$为度为$1$的结点数，易知：$n=n_0+n_1+n_2$①
  • 设$B$为分支数，则有$n=B+1$(考虑边数，每个结点都有“来自其父节点的边”，除了根节点，所以结点数是分支数+1)
    • 而又因为分支由$n_1,n_2$射出，所以$B=n_1+2\times n_2$
    • 两式可得$n=n_1+2n_2+1$②
  • 根据①，②得$n_0=n_2+1$

  • 顺便一说，此处的$B$(分支数)同样等于非$null$的指针数(如果是常规的、由各节点构成的二叉树)

1.2.2 完全二叉树

也就是除了最下面一层外，其余层都是满的二叉树，并且即使是最下面一层，也是从左到右排列的。

• 性质
  • 叶子结点只可能出现在层次最大的两层中
  • 具有$n$个结点的完全二叉树的深度为$\lfloor\log_2 n\rfloor+1$（下取整）

    证明：$2^{k-1}-1< n \leq 2^k-1$，两边同取对数就能得到了

  • 结点编号规律(如果按照层次编号)：
    • 若$i=1$，则为根结点
    • 若$i>1$，则其父结点为$\lfloor i/2 \rfloor$
    • 若$2i \leq n$，则其左孩子为$2i$，右孩子为$2i+1$

      证明略

1.2.3 二叉树的顺序存储结构

在这种存储结构中，最重要的问题是存储结构中的序号如何与结点的位置对应起来

• 完全二叉树

因为上面刚说过的，完全二叉树天生层次编号的话有规律，就直接按照层次编号存储就好

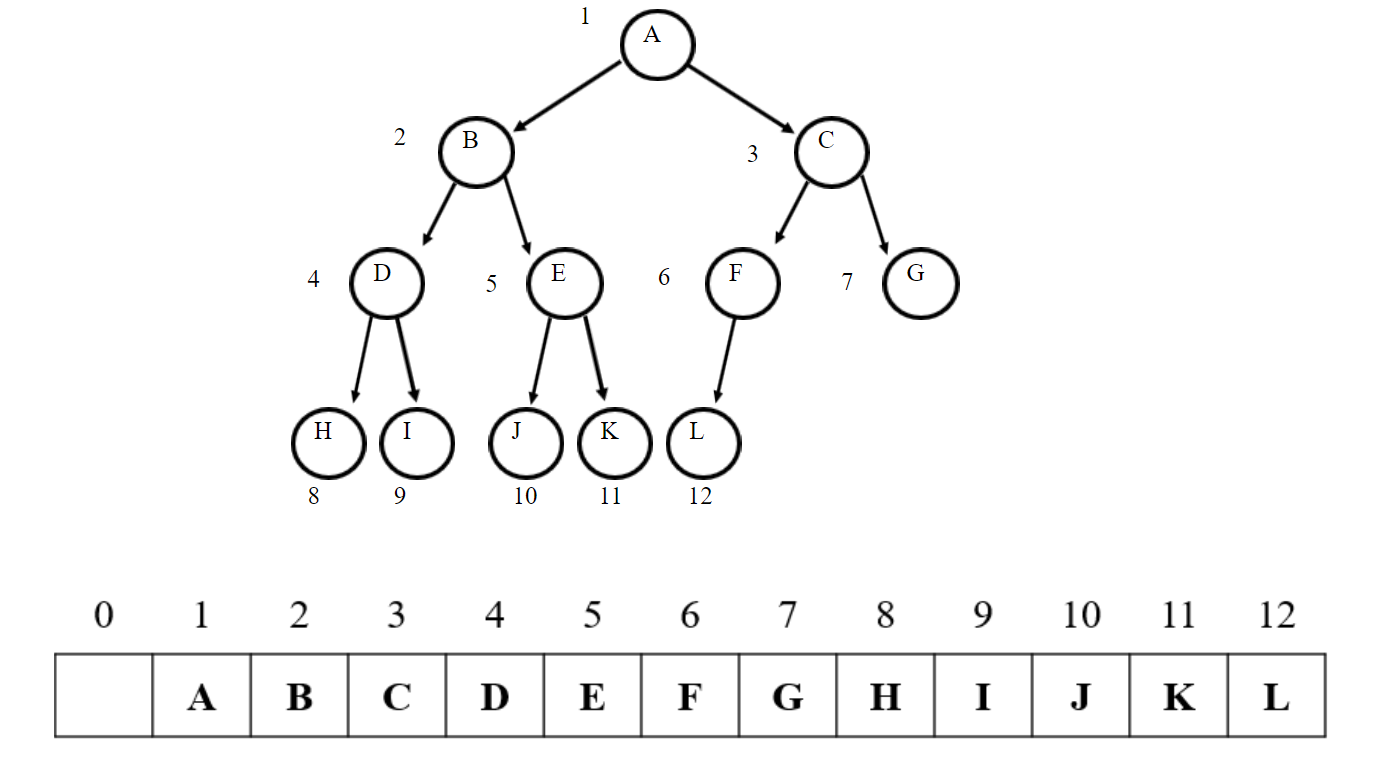
• 如果是按照上述存储结构，放弃list[0]直接从list[1]开始，那么完全二叉树的顺序存储完全遵循上述层序编号的规律。对于结点$i(i \geq 1)$，其左子结点为list[2*i]，右子结点为list[2*i+1]，父结点为list[i//2]。

• 普通二叉树

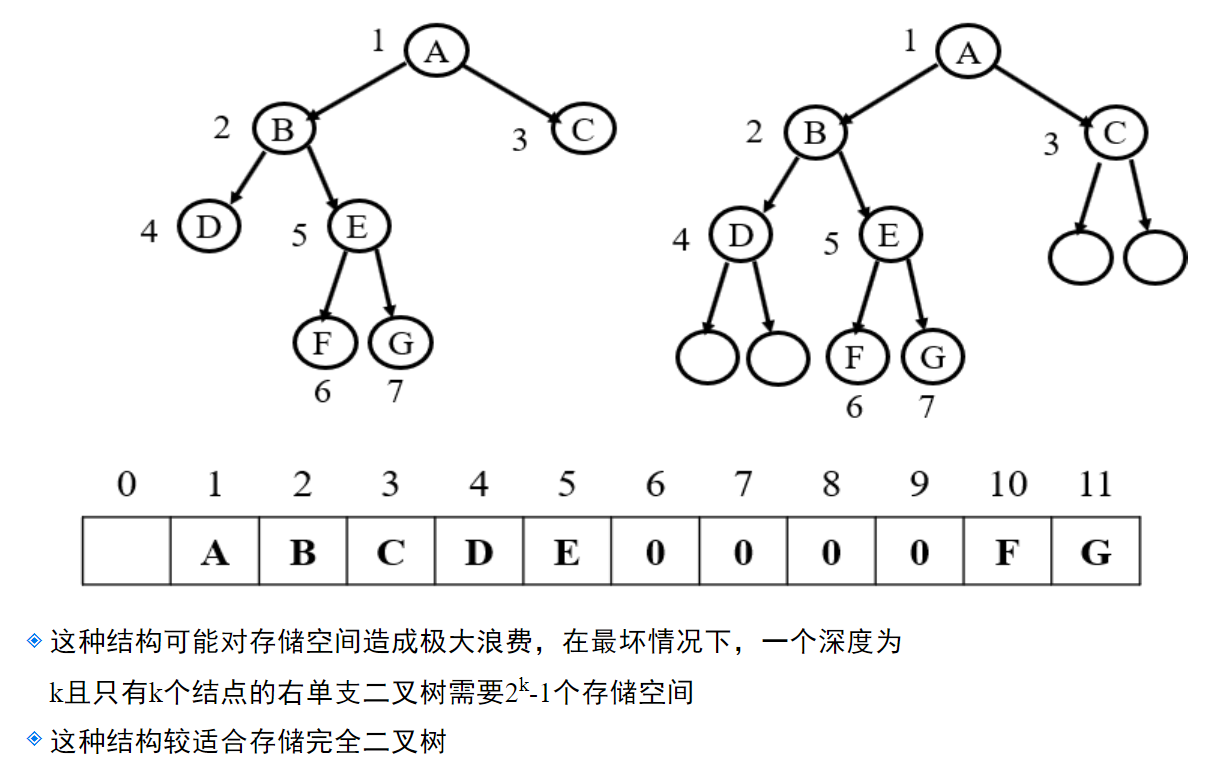
如果硬是要仿照完全二叉树的结构来存储，也不是不行，但对于普通二叉树来说会造成空间的巨大浪费。

所以对于普通二叉树，通常采用链式存储。

1.2.4 二叉树的链式存储结构

注意，本小节以及衍生的遍历方法均为重点。

(1) 数据结构定义

在树的链式存储中，我们通常是直接存储树的各个结点，每个结点存储其数据元素以及指向其他结点的指针。

通常结点至少要包含“指针域”和“数据域”。指针域即指向lChild和rChild的指针，数据域即该结点的数据，这种存储结构被称为二叉链表。而如果还包括指向父结点的指针，则被称为三叉链表。

• C Version

// 二叉链表
typedef struct BiTNode {
  TElemType data;
  struct BiTNode *lChild = NULL;
  struct BiTNode *rChild = NULL;
} BiTNode, *BiTree;

// 三叉链表
typedef struct BiTNode {
  TElemType data;
  struct BiTNode *lChild = NULL;
  struct BiTNode *rChild = NULL;
  struct BiTNode *parent = NULL;
} BiTNode, *TriTree;

• Python Version

# 二叉链表
class BiTNode:
  def __init__(self, data):
    self.data = data
    self.lChild = None
    self.rChild = None

# 三叉链表
class BiTNode:
  def __init__(self, data):
    self.data = data
    self.lChild = None
    self.rChild = None
    self.parent = None

• Java Version

// 二叉链表
class BiTNode {
  public BiTNode (TElemType data) {
    this.data = data;
    this.lChild = null;
    this.rChild = null;
  }
}

// 三叉链表
class BiTNode {
  public BiTNode (TElemType data) {
    this.data = data;
    this.lChild = null;
    this.rChild = null;
    this.parent = null;
  }
}

1.2.5 遍历二叉树

遍历二叉树其实是一种递归算法。假如我们遍历的操作只是打印值，那么根据向左走、执行操作、向右走(其实还有一个隐式的回溯)这几个操作的先后顺序，分为前(先)序遍历、中序遍历、后序遍历三种结果。

(1) 前序遍历

三种动作的优先级为执行操作(打印)>向左走>向右走。执行结果为A B D E F G C

(2) 中序遍历

三种动作的优先级为向左走>执行操作(打印)>向右走。执行结果为D B F E G A C

(3) 后序遍历

三种动作的优先级为向左走>向右走>执行操作(打印)。执行结果为D F G E B C A

遍历顺序演示

三种遍历方法的路径其实都是这个，只不过打印的策略有所不同罢了

代码参考

• C Version

void PreOrder(BiTree T)
{
  if (T != NULL)
  {
    printf("%c ", T->data);
    PreOrder(T->lChild);
    PreOrder(T->rChild);
  }
}

void InOrder(BiTree T)
{
  if (T != NULL)
  {
    InOrder(T->lChild);
    printf("%c ", T->data);
    InOrder(T->rChild);
  }
}

void PostOrder(BiTree T)
{
  if (T != NULL)
  {
    PostOrder(T->lChild);
    PostOrder(T->rChild);
    printf("%c ", T->data);
  }
}

• Python Version

def PreOrder(T: BiTNode):
    if T is not None:
        print(T.data, end=" ")
        PreOrder(T.lChild)
        PreOrder(T.rChild)


def InOrder(T: BiTNode):
    if T is not None:
        InOrder(T.lChild)
        print(T.data, end=" ")
        InOrder(T.rChild)


def PostOrder(T: BiTNode):
    if T is not None:
        PostOrder(T.lChild)
        PostOrder(T.rChild)
        print(T.data, end=" ")

例题

例题1：二叉树基本概念

在一棵度数为4的树T中，若有20个度为4的结点，10个度为3的结点，1个度为2的结点，10个度为1的结点，则树T的叶结点个数是()

参考资料

• 《数据结构 第6章 树与二叉树》(课程PPT) by 云南大学 信息学院 陈老师