[工程数学]1 复数与复变函数

我上高中时，我的老师常挂在嘴边一句话：“基础不牢，地动山摇”，现在越发深以为然。虽然工程数学是一门数学学科，做题技巧很重要，但打好基础比刷题重要100倍！

Steven-Zhl 头像
[工程数学]1 复数与复变函数

复变函数第一章，主要内容是各种基础概念与知识点。

1.1 复数

  • 符号约束
    • $z$: 复数,，在后续的学习中，不明确说明的话，就认为$z=x+\text{i}y$
    • $x,y$: 实部/虚部，均为实数
    • $\text{i}$: 虚数单位，满足$\text{i}^2=-1$
    • $\theta$: 辐角(通常直接认为是主辐角)，满足$-\pi<\theta\leq\pi$
    • $G$: 平面点集(不常用)
    • $D$: 区域

1.1.1 复数的基本概念

  • 复数: 按照一般习惯，我们通常用$z=x+\text{i}y$来表示一个复数，其中：
    • $x$为实部
    • $y$为虚部
    • $\text{i}$为虚数单位，且满足$\text{i}^2=-1$
  • 共轭复数: 这是个相对概念，若一个复数$z=x+\text{i}y$，则其共轭复数为$\overline{z}=x-\text{i}y$，反之亦然
  • 实部(函数): $\text{Re}()$，这是个函数，输入是一个复数，输出是复数的实部，也就是说$\text{Re}(z)=x$

1.1.2 复数的四则运算

就类似于高中数学中的向量的加减法，所以在后续的学习中，复数的形象化表示就是将其作为向量画出来。

假定$z_1=x_1+\text{i}y_1,z_2=x_2+\text{i}y_2$

  • 加法: $z_1+z_2=(x_1+x_2)+\text{i}(y_1+y_2)$
  • 减法: $z_1-z_2=(x_1-x_2)+\text{i}(y_1-y_2)$
  • 乘法: $z_1 \cdot z_2=x_1x_2+\text{i}x_1y_2+\text{i}x_2y_1-y_1y_2$(就是简单的二项式乘法)
  • 除法: $z_1/z_2$，此处我们要回顾一个定律：$(a-b)(a+b)=a^2-b^2$，根据此，我们可以用$z_1\overline{z_2}/z_2\overline{z_2}$计算，此时分母已经是一个实数了($x_2^2-y_2^2$)，也就可以计算了

1.1.3 复平面

复平面就是复数可视化的一种实现方法，后续的学习中我们会非常经常地用到复平面。

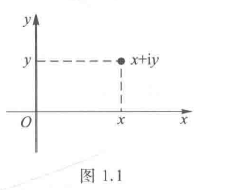
  • 复平面是复数可视化的一种实现方法，具体来讲是将复数视为一个二维平面中的点，实部为$x$轴的值，虚部为$y$轴的值。 复数的平面表示
  • 此外，由于上面提到的四则运算其实和二维向量的四则运算是一样的，为了之后计算的方便，其实将复数视为一个二维向量是更常见的做法。

1.2 复数的三角表示

1.2.1 复数的模(模长)与辐角

  • 上一节其实已经说过了，复数最常用的表示方法就是将其视为一个二维向量，通常我们将其表示为$\overrightarrow{Oz}$。 复数的向量表示

  • 既然是个向量，那么有一些向量的概念也是可以用到复数上的，比如模(模长)与辐角。

  • 模: $\vert z \vert=\sqrt{x^2+y^2}$，向量的模长(长度)，也就是复数到原点的距离
  • 辐角: $\text{Arg} z$，实轴正向与向量$\overrightarrow{Oz}$的夹角。
    • 显而易见的是，辐角有无穷多个值，彼此相差$2k\pi$。为了方便，我们常用的是主辐角
    • 主辐角: $\arg{z}$，在无穷个辐角中，只取$(-\pi,\pi]$中的那个作为主辐角。

1.2.2 复数模的三角不等式

根据先前的课后题，以及考试经验来说，三角不等式似乎没怎么考过…

  • 在高中时期我们学到一个三角不等式，用自然语言描述为:
    1. 三角形中两边之和大于第三边
    2. 三角形中两边之差小于第三边
  • 而这个三角不等式同样可以推到平面向量以及复数中。 复数模的三角不等式
  • 根据上面两图，可以得到复数模的三角不等式:
    • $\vert z_1+z_2 \vert \leq \vert z_1 \vert + \vert z_2 \vert$
    • $\vert z_1-z_2 \vert \geq \vert z_1 \vert - \vert z_2 \vert$

1.2.3 复数的三角表示

三角表示是个重点，后面的公式与定理中中大量用到了复数的三角表示

为了方便，我们通常约定$\theta$就是主辐角，就一个值，不会有多个值。

  • 复数的三角表示: $z=r(\cos{\theta}+\text{i}\sin{\theta})$

    不难看出：$r$实际上就是模长，$\theta$实际上就是辐角，这也是我们为什么要学这个：在平面几何中这个表示方法尤其有用。

  • 复数的指数形式: $z=r\text{e}^{\text{i}\theta}$

    在某些情况下，复数的指数形式会很有用，比如在求复数的幂的时候。

1.2.4 用复数的三角表示作乘除法

1.2.5 复数的乘方与开方

(1) 乘方

\[z^n=[r(\cos{\theta}+\text{i}\sin{\theta})]^n=r^n(\cos{n\theta}+\text{i}\sin{n\theta})\]

刨去$r^n$的部分，这个公式被称为棣莫弗公式。

这个可以用欧拉公式轻松证明：$r\text{e}^{\text{i}\theta}=r(\cos{\theta}+\text{i}\sin{\theta})$，因此$[r(\cos{\theta}+\text{i}\sin{\theta})]^n=[r\text{e}^{\text{i}\theta}]^n=r^n\text{e}^{\text{i}\theta n}$，此时将$\theta n$视为一个整体，得到$r^n(\cos{n\theta}+\text{i}\sin{n\theta})$。

  • 这个公式的意义在于，在面对复数的乘方时，我们可以观察实部和虚部是否能够凑成$\cos{\theta}$和$\sin{\theta}$(也就是三角形式)，然后再转为复数形式，这样就可以简化乘方计算了。

(2) 开方

  • 设$z=r\text{e}^{\text{i}\theta},w=\rho \text{e}^{\text{i}\varphi},w^n=z$
  • 则根据乘方法则，可以知道$\rho^n\text{e}^{\text{i}n\varphi}=r\text{e}^{\text{i}\theta}$，即得到$\rho^n=r,\rho=^n\sqrt{r}$

1.3 平面点集的一般概念

1.3.1 开集与闭集

按照以往经验来看，本小节的内容考的很少….不是考试重点，但是从知识脉络的角度来看，是挺重要的，因为后面的一些概念都是基于这个的。

  • 符号约束：
    • $G$:平面点集
    • $z_0$:$G$中的任意一点
  • $\vert z - z_0 \vert < \delta$: 表示$z_0$的邻域，可以看得出来，就是与$z_0$所有距离小于$\delta$的点的集合
  • 内点: 若$z_0$的邻域的点都属于$G$，则$z_0$是$G$的内点，也就是说“只有一个点和它的邻居都属于$G$，它才是$G$的内点”
  • 边界点: 从定义上就和内点反着来的，若$z_0$的任一邻域内既有$G$的点又有$\complement G$的点，也就是说$z_0$在$G$与$\complement G$之间，但它仍然属于$G$
  • 开集&闭集: 若$G$中的每一点都是$G$的内点，则$G$是开集，否则是闭集

    直观理解呢，“开集”给人一种“挑剔”的感觉：所有点都是我的内点及其邻居都在我的范围内，才可称开集。但由于这一点，开集有些不确切和难以想象；闭集相比之下就常见很多：随便画一个闭合图形，它的内部是内点，它的边界是边界点，这些全部包括起来就是闭集。

    • 举个例子，$G$是一个圆，那么$G$是开集，因为圆内的每一点都是圆的内点
    • 举个例子，$G$是一个圆的边界，那么$G$是闭集，因为圆的边界上的点都是圆的边界点
  • $\complement G$: $G$的余集，即平面上不属于$G$的所有点构成的集合
  • 有界集、无界集实在没什么使用价值，就不说了

1.3.2 区域

“在今后的讨论中，变化范围主要是指区域”，因此我们有必要了解一下区域的概念。

  • 平面点集$D$称为一个区域，如果它满足下列两个条件：
    1. $D$是一个开集
    2. $D$是连通的，就是说$D$中任意两点都可以用一条折线连起来，这条折线的每一段都在$D$内部。
  • 换言之，区域就是连通开集

上一节刚说过，开集有些不确切和难以想象。是因为作为一个集合，它没有边界，若这个集合的点还是连续的，那就是“一团混沌”了。现在给出的“连通开集”则更是说明了这一点：“连续的一团混沌”。从这里开始，值域从离散的集合正式转变为连续的区域，以后在面对复变函数时，不需要再想集合了，直接想一个完整的区域即可。

1.3.3 平面曲线

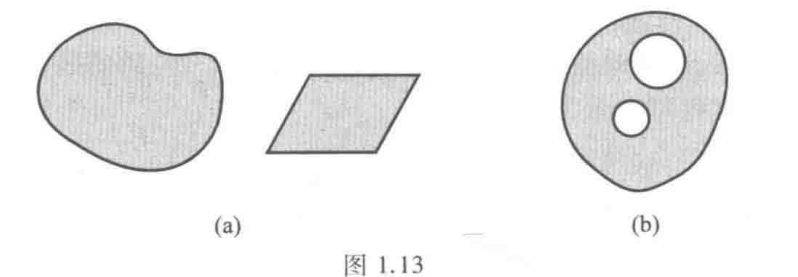
  • 设$D$是一区域，如果对$D$内的任一简单闭曲线，曲线的内部总属于$D$，则称$D$是单连通区域，不是单连通区域称为多(复)连通区域。

    简单闭曲线：闭合的曲线，且不自交，也就是说，它不会有“洞”

    单连通区域：没有“洞”的区域

    多连通区域：有“洞”的区域

单连通区域与多连通区域

1.4 无穷大与无穷远点

这一节实在没啥意思，就不整理了

1.5 复变函数

这一节才算第一章的核心内容。

1.5.1 复变函数的概念

就是把变量从实数变为了复数。从第一反应来说，这个函数有点像是二元函数/曲面积分，因为毕竟一个复数就是两个部分的组合。但细细想来，是不太一样的，因为曲面积分中，$z=f(x,y)$，而这里是$w=u(x,y)+\text{i}v(x,y)$

\[w=f(z),z \in D,w\text{也为复数}\] \[w=u+\text{i}v=f(x+\text{i}y)=u(x,y)+\text{i}v(x,y)\]
  • 上面的第2个表示法是最常用的(1式几乎没用过)，2式的在于构建了二元形式的映射关系，注意$x,y$本身是$z$的组成部分，但在$w$中却成了实部和虚部的参数。
  • 其他的什么像、原像等概念都是从映射的角度理解函数的，这里就不说了，因为我们后面研究的复变函数实际上都是真正意义上的“函数”了

1.5.2 复变函数的极限

  • 设函数$w=f(z)$在$z_0$的去心邻域$0<\vert z-z_0\vert <\rho$内有定义，​若存在复数​$A\not ={\infty},\forall{\epsilon}>0,\exists{\delta}>0$，使得当$0<\vert z-z_0\vert\delta$时，有$\vert f(z)-A\vert <\epsilon$，则称$A$为函数$w=f(z)$当$z$趋向于$z_0$时的极限，记作
\[\lim_{z\rightarrow z_0}f(z)=A\]
  • 注：
    • 此时$f(z)$在$z_0$可以无定义
    • $z$以任意方式趋向于$z_0$都得到$A$(常用这一点证明极限不存在)

每次看到极限的定义我都觉得这个公式很难理解。算了就别理解了，跟高数第一章极限的定义一样，这个极限也与之类似。

(1) 极限的性质

若$\lim\limits_{z\rightarrow z_0}f(z)=A,\lim\limits_{z\rightarrow z_0}g(z)=B$

  • $\lim\limits_{z\rightarrow z_0}[f(z)\pm g(z)]=A\pm B$
  • $\lim\limits_{z\rightarrow z_0}[f(z)\cdot g(z)]=A\cdot B$
  • $\lim\limits_{z\rightarrow z_0}\frac{f(z)}{g(z)}=\frac{A}{B},(B\not ={0})$

(2) 两个常考的极限定义的问题

这2个问题也在高数中常常被问到，详见例题E1.1

  1. 如何证明极限存在？
    • 放大技巧：$\vert f(z)-A \vert\leq g(\vert z-z_0 \vert)$
  2. 如何证明极限不存在？
    • 选择不同的路径趋近于$z_0$，得到不同的极限值。即“极限值与路径有关”，则证明极限不存在。

1.5.4 复变函数的连续

  • 若$\lim\limits_{z \rightarrow z_0}f(z)=f(z_0)$，则称$f(z)$在$z_0$点连续。

看得出来，连续其实比极限存在更苛刻，连续是在极限存在的基础上，$f(z_0)$还要存在且等于极限值，而连续则不要求$f(z_0)$存在。

  • 因此：连续则极限一定存在，极限存在不一定连续。

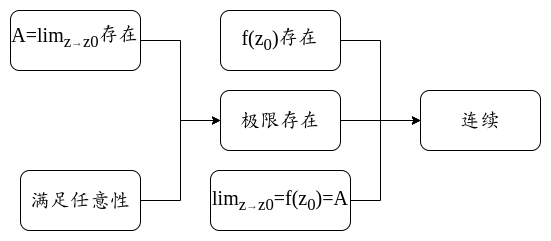
连续与极限

  • 此外还可以推出一个定理：函数$f(z)=u(x,y)+\text{i}v(x,y)$在$z_0=x_0+\text{i}y_0$处连续的充要条件是$u(x,y)$和$v(x,y)$在$(x_0,y_0)$处连续。

例题

E1.1 证明极限存在&极限不存在

相关知识点：函数极限存在需满足路径任意性

  • 讨论函数$f(z)=\frac{\bar{z}}{z}$在$z\rightarrow{0}$的极限
\[f(z)=\frac{x-\text{i}y}{x+\text{i}y}\] \[\text{当}y=0,x\rightarrow 0\text{时},f(z)\rightarrow 1\] \[\text{当}x=0,y\rightarrow 1\text{时},f(z)\rightarrow -1\] \[\text{因此极限不存在}\]
  • 试证：$\lim\limits_{z\rightarrow 0}\frac{\text{Re} z}{z}$不存在
\[\text{设}z=x+\text{i}y,\text{原式可化为}\lim_{z\rightarrow 0}\frac{x}{x+\text{i}y}\] \[=\lim_{z\rightarrow 0}\frac{x(x-\text{i}y)}{x^2+y^2}\] \[\text{当}x=0,y\rightarrow 0\text{时},\lim_{z\rightarrow 0}\frac{x(x-\text{i}y)}{x^2+y^2}=0\] \[\text{当}y=0,x\rightarrow 0\text{时},\lim_{z\rightarrow 0}\frac{x(x-\text{i}y)}{x^2+y^2}=1\] \[\text{故该极限不存在}\]