[工程数学]3 复变函数的积分

上午上完工程数学，下午写笔记，凉性循环~

Steven-Zhl 头像
[工程数学]3 复变函数的积分

本章讲的是复变函数的相关积分，不过重点直接就是曲线积分了。这一章只看知识点其实也不算很多，但重点是题型太多了，要多做题熟悉熟悉。

此外这一章PPT比较生草的是，在第二节讲柯西积分定理时，积分范围的形状直接套用的湖北省地图和陕西省地图…

graph LR 复变函数的积分 --> 复积分的概念 复变函数的积分 --> 柯西积分定理

3.1 复积分的概念

3.1.1 复积分的定义

算了别记了，反正也不考，而且又是个通过极限给出的定义

  • $\int_{C^-}f(z)\text{d}z$表示沿曲线$C$的负方向积分(在曲线积分里，曲线是有向的)
  • $\oint_\Gamma f(z)\text{d}z$表示沿闭曲线$\Gamma$的正方形(逆时针方向)积分

3.1.2 复积分的性质

和实变函数曲线积分的性质高度相似

  1. $\int_C [\alpha f(z)+\beta g(z)]\text{d}z=\alpha\int_C f(z)\text{d}z+\beta\int_C g(z)\text{d}z$
  2. $\int_C f(z)\text{d}z=-\int_{C^-}f(z)\text{d}z$
  3. $\int_C f(z)\text{d}z=\int_{C_1}f(z)\text{d}z+\int_{C_2}f(z)\text{d}z,\text{其中}C=C_1+C_2$
  4. $\vert\int_C f(z)\text{d}z\vert\leq \int_C\vert f(z)\vert\vert\text{d}z\vert=\int_C\vert f(z)\vert\text{d}s\leq ML\text{其中}M=\max\limits_{z\in C}\vert f(z)\vert,L\text{为曲线}C\text{的弧长}$

3.1.3 复积分的计算

告诉你2种如何计算复积分的方法

(1) 化为第二类曲线积分

\[\int_C f(z)\text{d}z=\int_C(u+\mathrm{i}v)(\text{d}x+\mathrm{id}y)=\int_C u\text{d}x-v\text{d}y+\mathrm{i}\int_C v\text{d}x+u\text{d}y\]
  • 随后可进一步化为定积分或二重积分以计算
  • 但通常不会这么干，因为一旦知道了$C$关于$x,y$的表达式，用下一种计算方法更简单

(2) 直接化为定积分

设曲线$C:z=z(t)=x(t)+\mathrm{i}y(t),t:a\rightarrow b$，则有：

\[\int_C f(z)\text{d}z=\int^b_a f\left[z(t)\right]z'(d)\text{d}t,\text{其中},z'(t)=x'(t)+\mathrm{i}y'(t)\]
  • 通常更倾向于使用这种方法计算，因为确实简单，前提是$z$关于$t$或者$z$关于$(x,y)$的表达式要看得出来才行。

(3) 其他方法

3.2 柯西积分定理

柯西积分定理是整个第3章的基础，也是在此基础上，发展出了本章的所有的解题方法。本章知识点不多，但是题型很多，所以要多做题。

3.2.1 柯西基本定理

但是要说的是，柯西基本定理其实不能直接拿来计算积分，看过就发现，它直接的作用是说“解析函数沿着闭合曲线的积分结果为0”，这句话是没法拿来计算的。后续基于柯西基本定理开发出的其他方法才是实现“计算任意曲线积分”的关键。

(1) 柯西基本定理(柯西-古萨基本定理)

湖北省1

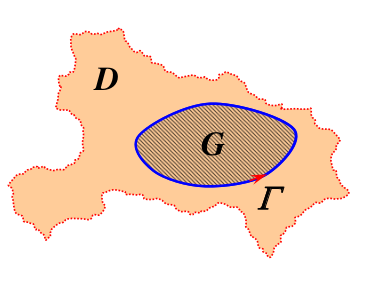
  • 公式描述：设函数$f(z)$在单连通域$D$内解析，$\Gamma$为$D$内任意一条简单闭曲线，则有：
\[\oint_\Gamma f(z)\text{d}z=0\]
  • 语言描述：若某函数在一个单连通域内解析(处处可导)，则该函数沿域内任意一条简单闭曲线的积分为0。
  • 还记不记得在实变函数中，曲线积分的结果与路径无关，只与起点和终点有关？这里也是类似，闭合曲线的起点和终点相同，故积分为0。有点像高中物理，向量走一圈回到原点，位移为0。

(2) 柯西基本定理引理

相比于柯西基本定理，引理将曲线$\Gamma$扩展到了积分区域的边界$C$，现在应用柯西基本定理不必再限制在区域$D$内了

湖北省2

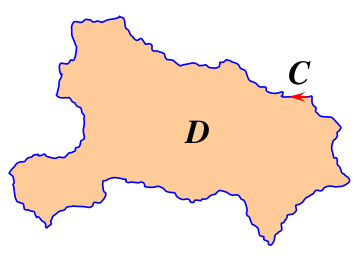
  • 公式描述：设函数$f(z)$在单连通域$D$内解析，在$\bar{D}=D+C$上连续，其中$D$的边界为$C$，则有：
\[\oint_C f(z)\text{d}z=0\]

3.2.2 闭路变形原理

(1) 柯西基本定理引理2

此处引理是将柯西基本定理推广到了二连域的结果

陕西省1

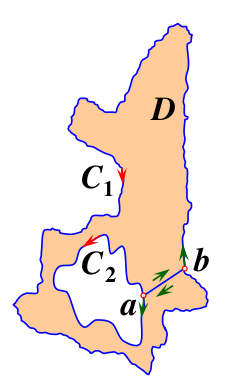
  • 公式描述：设二连域的边界为$C=C_1+C_2^-$(之所以表示为$C_2^-$是因为边界有正负向之分，逆时针为正向，顺时针为负向，以后面对二连域或者n连域均采用这种表示，外部边界正向，内部边界反向，且用正负号作为区分)，函数$f(z)$在$D$内解析，在$C$上连续，则有：
\[\oint_C f(z)\text{d}z=\oint_{C_1} f(z)\text{d}z+\oint_{C_2^-} f(z)\text{d}z=0.\] \[\text{也可得}\oint_{C_1} f(z)\text{d}z=\oint_{C_2} f(z)\text{d}z\]

这个定理已经暗含了计算曲线积分的方法了：如果要计算$\oint_{C}f(z)\text{d}z$，那么在范围$D$内构建一个新的边界$C’$，与$C$反向，通过计算$\oint_{C’}f(z)\text{d}z$来得到结果。至于$C’$怎么构造嘛，肯定是怎么好算怎么来。

(2) 闭路变形原理

闭路变形原理是对上面的几个定理归纳得出的结果，但就实用程度来说，不如柯西基本定理引理2

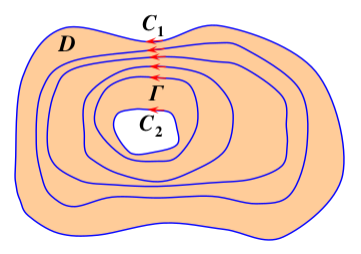
闭路变形原理

  • 语言描述：在区域内的一个解析函数沿闭曲线的积分，不因闭曲线在区域内作连续变形而改变它的值(解析函数在区域内沿任意闭合曲线的积分值都相同)

3.2.3 复合闭路定理

将柯西基本定理(更准确来说应该是柯西基本定理引理2)推广到多连域，但其实我们熟悉了之后会发现，这一系列定理都是一脉相承的。

  • 公式描述：设多连域$D$的边界为$C=C_0+C_1^-+C_2^-+…+C_n^-$，函数$f(z)$在$D$内解析，在$C$上连续，则有：
\[\oint_C f(z)\text{d}z=0\]

$\text{或者说}\oint_{C_0}f(z)\text{d}z=\oint_{C_1}f(z)\text{d}z+\oint_{C_2}f(z)\text{d}z+…+\oint_{C_n}f(z)\text{d}z$

3.2.4 路径无关性

路径无关性是上述一堆柯西积分定理变形的核心思想。

  • 自然语言描述：设函数$f(z)$在单连通域$D$内解析，$C_1,C_2$为$D$内的任意两条从$z_0$到$z_1$的简单曲线，则有$\int_{C_1}f(z)\text{d}z=\int_{C_2}f(z)\text{d}z$

3.2.5 原函数

其实就是牛顿-莱布尼茨公式。对我来说这一节不用太过留意，因为$f(z)$通常很难直接计算原函数，而容易计算出来的又不用特意想着，顺手就算出来原函数了。

  • 设在单连域$D$内，函数$F(z)$恒满足条件$F’(z)=f(z)$,则$F(z)$称为$f(z)$在$D$内的一个原函数
  • 此时可以使用牛顿-莱布尼茨公式计算积分：$\int_{z_0}^{z_1}f(z)\text{d}z=F(z)\bigg\vert^{z_1}_{z_0}$

3.3 柯西积分公式

3.3.1 柯西积分公式

这个公式建议…直接背下来，证明思路太过复杂，用到了类似极限定义的方法，我是有点看不懂的…

但大概思路大致就是上面说过的柯西基本定理引理2，只不过直接把积分路径固定为了一个圆形边界，相对好算。

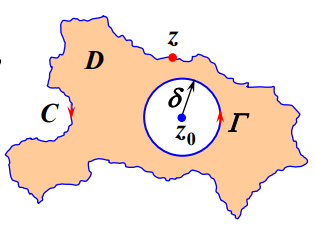
工程数学-湖北省3

  • 定理：如果函数$f(z)$在区域$D$内解析，在边界$C$上连续，$z_0 \in D$，则：
\[f(z_0)=\frac{1}{2\pi\text{i}}\oint_C\frac{f(z)}{z-z_0}\text{d}z\]
  • 那么这个公式有什么用呢？其实并不是直接这么用的，最常用的用法是：$\oint_C \frac{f(z)}{z-z_0}\text{d}z=2\pi\text{i}f(z_0)$，若一个函数$g(z)$能配凑成$\frac{f(z)}{z-z_0}$的形式，那么就可以直接用这个公式计算积分了。

3.4 解析函数的高阶导数

3.4.1 高阶导数定理

  • 如果函数$f(z)$在区域$D$内解析，在$\bar{D}=D+C$上连续，则$f(z)$的各阶导数均在$D$上解析，且：
\[f^{(n)}(z_0)=\frac{n!}{2\pi\text{i}}\oint_C \frac{f(z)}{(z-z_0)^{n+1}}\text{d}z,(z_0\in D)\]

这个公式不是很泛用，只是遇到了$f^{(n)}(z)$或者$\oint_C\frac{f(z)}{(z-z_0)^n}\text{d}z$这种高阶函数时用一下就行。

例题

E3.1 计算$I=\int_C z\text{d}z$，其中$C$为(如图)

例题3.1

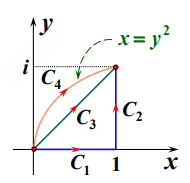
相关知识点：复变函数的计算-直接化为定积分，注意要想到：$\text{d}z=\text{d}x,\text{d}z=\text{id}y$，因为$z=x+\text{i}y$

(1) $C=C_1+C_2$

易知：$C_1:z=x,x:0\rightarrow 1;C_2=1+\text{i}y,y:0\rightarrow 1$

  • $I=\int_{C_1}z\text{d}z+\int_{C_2}z\text{d}z$
  • $=\int^1_0 x\text{d}x+\int^1_0 (1+\text{i}y)\text{i}\text{d}y$
    • (这里第二部分的换元实质上是$(1+\text{i}y)\text{d}(1+\text{i}y)=(1+\text{i}y)\frac{\partial 1+\text{i}y}{\partial y}\text{d}y=\text{i}(1+\text{i}y)dy$，跳步了注意一下)
  • $=\frac{x^2}{2}\bigg\vert^1_0+(\mathcal{i}y-\frac{1}{2}y^2)\bigg\vert^1_0=\mathcal{i}$

(2) $C=C_3$

易知：$C_3:z=t+\text{i}t,t:0\rightarrow 1$

  • $I=\int_{C_3}z\text{d}z$
  • $=\int^1_0 (t+\text{i}t)(1+\text{i})\text{d}t$
  • $=(1+\text{i})(1+\text{i})\int^1_0 t\text{d}t$
  • $=2\text{i}\cdot \frac{1}{2}t^2\bigg\vert^1_0=\text{i}$

(3) $C=C_4$

这里我们当然可以看出来$C_4$可以表示为$C_4:z=x+\text{i}y,y:0\rightarrow 1,x=y^2$，但这里统一以$t$表示是个更简便的选择：$C_4:z=t^2+\text{i}t,t:0\rightarrow 1$

  • $I=\int_{C_4}z\text{d}z$
  • $=\int^1_0 (t^2+\text{i}t)(2t+\text{i})\text{d}t$
  • $=(\frac{1}{2}t^4+\text{i}t^3-\frac{1}{2}t^2)\bigg\vert^1_0$
  • $=\text{i}$

E3.2 计算积分$\oint_C \frac{\bar{z}}{|z|}\text{d}z$的值，其中$C$为：(1) $|z|=2$；(2) $|z|=4$

相关知识点：复变函数的计算-直接化为定积分，[技巧]遇到$\vert z \vert$的积分时，将$z$转换为指数表示($z=re^{\text{i}\theta},\vert z \vert =r$)会简便很多

\[\text{设}z=re^{\text{i}\theta}\] \[\text{则}\oint_C \frac{\bar{z}}{|z|}\text{d}z=\int_0^{2\pi}\frac{re^{-\text{i}\theta}}{r}r\text{i}e^{\text{i}\theta}\text{d}\theta=r\text{i}\int_0^{2\pi} 1 \text{d}\theta=2\pi r\text{i}\] \[\text{由题意知，当}|z|=2\text{时},r=2,\text{原式}=4\pi\text{i};\text{当}|z|=4\text{时},r=4,\text{原式}=8\pi\text{i}\]

E3.3 计算$\oint_C \frac{1}{z^2-z}\text{d}z$，其中$C$为圆周$|z|=2$

相关知识点：复合闭路定理，[一个推论]对于$\oint_C\frac{1}{(z-z_0)^n}\text{d}z$，若$n=1$，则结果为$2\pi\text{i}$，若$n\neq 1$，则结果为$0$，这其实是根据柯西积分公式和高阶积分公式推出来的，用上这个公式的话能省不少时间。

(1) 常规解法：复合闭路定理

\[f(z)=\frac{1}{z^2-z}=\frac{1}{z(z-1)}\text{在}|z| \leq 2\text{的范围内有两个奇点：}z=0\text{和}z=1\] \[\text{分别以该两点为圆心作圆周}C_1,C_2,\text{且两圆周不相交，可得：}\] \[\oint_C \frac{1}{z^2-z}\text{d}z=\oint_{C_1}(\frac{1}{z-1}-\frac{1}{z})\text{d}z+\oint_{C_2}(\frac{1}{z-1}-\frac{1}{z})\text{d}z\] \[\text{由于}C_1\text{中不包含}\frac{1}{z-1}\text{的奇点，所以这部分积分值为}0,\text{而由于包含}\frac{1}{z}\text{的奇点，所以积分值为}-2\pi\text{i}\] \[\text{后面这部分同理，积分值为}2\pi\text{i}\] \[\text{两部分之和为}0\]

(2) 推论解法

\[\oint_C \frac{1}{z^2-z}\text{d}z=\oint_C (\frac{1}{z-1}-\frac{1}{z})\text{d}z\] \[\text{根据推论，这两部分均符合}n=1\text{的情况}\] \[\text{所以结果为}2\pi\text{i}-2\pi\text{i}=0\]

E3.4 计算$\oint_{\vert z-\text{i}\vert=1}\frac{\text{d}z}{z^2-\text{i}}$

相关知识点：复数的开方，柯西积分公式

  • 根据第一章所讲的复数开方的方法，设$w=\rho e^{\text{i}\varphi} ,w^2=\text{i}$
  • 易知此时$\text{i}$可以表示为$e^{\text{i}\frac{\pi}{2}}$
  • 联立得$\rho^2e^{\text{i}\cdot 2\varphi}=e^{\text{i}\frac{\pi}{2}}$，故$\rho=1,\varphi=\frac{\pi}{4},w=\sqrt{\text{i}}=e^{\frac{\pi}{4}\text{i}}$
\[\oint_{\vert z -\text{i} \vert =1}\frac{\text{d}z}{z^2-\text{i}}=\oint_{\vert z -\text{i} \vert =1}\frac{\text{d}z}{(z-e^{\frac{\pi}{4}\text{i}})(z+e^{\frac{\pi}{4}\text{i}})}\] \[\text{由于奇点}e^{\text{i}\frac{\pi}{4}}\text{对应到复平面中}(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})\text{的位置，在区域内，而}\frac{1}{z+e^{\text{i}\frac{\pi}{4}}}\text{在区域内解析}\] \[\text{所以使用柯西积分公式：}\] \[=\oint_{\vert z -\text{i} \vert =1} \frac{\frac{1}{z+e^{\frac{\pi}{4}\text{i}}}}{z-e^{\frac{\pi}{4}\text{i}}}\text{d}z=2\pi\text{i}\frac{1}{2e^{\text{i}\frac{\pi}{4}}}\] \[=\frac{\pi\text{i}}{\sqrt{2}+\sqrt{2}\text{i}}=\pi(\frac{\sqrt{2}}{2}+\text{i}\frac{\sqrt{2}}{2})\]